limites

mi nombre es Jairo José Montero Rodríguez nacido el 12 de diciembre del 2002 residente del municipio de Villanueva Guajira-Colombia, tengo 17 años de edad soy estudiante de ingeniería mecánica en la facultad de ingeniería en la Universidad de la Guajira

video de invitación

https://youtu.be/DBv-3iNddSk

INTRODUCCION

En este blog le daré a conocer todo lo relacionado con un gran tema como lo es el de limites,

uno de los análisis bases para estudiar una función su continuidad  y valores en el que posiblemente no este no exista, por lo tanto, estudiar a la función en un entorno ruidoso de valores y observando el comportamiento en ella misma.

limites

Los límites describen el comportamiento de una función conforme nos acercamos a cierto valor de entrada, sin importar el valor de salida de la función. La continuidad requiere que el comportamiento de una función alrededor de un punto sea igual al valor de la función en ese punto. 

para que exista un limite tota debe cumplirse la siguiente condición:

Una función f(x) tiene un limite cuando x se aproxima a c si y solo si los limites laterales izquierdo y derecho y a demás estos limites laterales sean iguales.

El valor del limite no depende de como se define la función en x=a, es decir:

Que en una función no importa que en su grafica presente una discontinua en un valor de x eso no significa que no tenga un valor, el valor si existe pero será diferente de a.

Las formas para hallar un limite son:

1° Por método grafico

2°  directamente desde la función

3° A través de tablas de valores

4° métodos matemáticos , cálculos o uso de formulas.

1° Por metodos gráficos

El método grafico consiste en encontrar el valor de f(x) por medio de una grafica, normalmente al presentarse este método contara con la función que dará paso a encontrar el limite.

Por ejemplo:

Suponiendo que la gráfica de la derecha es de la cual queremos encontrar el limite y tenemos esta función:

• Lim f(x)= 

  • x=0

Lo que tenemos que hacer es situarnos en el eje de las ¨x¨ en el punto 0, visualizando nuestra gráfica nos podemos dar cuenta que la función se puede acercar de ambos lados del punto 0 y el limite de la función se queda en 1.

 

si subimos en línea recta veremos que la función del limite f(x)= 1.

2° Directamente desde la función

Las funciones definidas a trozos son aquellas que están definidas en varios tramos, dependiendo del valor que tome la x. Al valor de la x donde la función cambia de tramo se le llama punto de ruptura y puede haber más de uno.

Pueden tener por ejemplo esta forma:

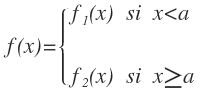
donde en este caso, el punto de ruptura sería el punto a.

En general, para resolver los límites de funciones, tenemos que sustituir la x por el valor al que tiende y después aplicar un método de cálculo u otro, dependiendo si resulta una indeterminación o no, como hemos visto en lecciones anteriores.

Sin embargo, en las funciones definidas a trozos, al tener varios tramos ¿en qué tramo debemos sustituir la x para resolver el límite? ¿Y cómo se resuelve el límite cuando la x tiende al punto de ruptura?

Vamos a ir respondiendo a estas preguntas al mismo tiempo que vamos resolviendo algunos ejercicios.

3° A través de tablas

1. 1) Haga una tabla de los valores de f(x) usando valores de x que se acerca a a por ambos lados.
2. 2) Si el límite existe, los valores de f(x) se acercarán al límite a medida que x se acerca a a por ambos lados.
3. 3) Cuanto más exacto desea estimar este límite, más cercano a a deberá elegir los valores de x.
4. 
   

4° Métodos matemáticos , cálculos o uso de formulas.

Algunos de los limites pueden ser limite finito, limite infinito y limite en el infinito:

LIMITE FINITO Y INFINITO

cálculos de limites defunciones funciones polinomicas :

 

cálculos de limites de funciones racionales, indeterminado:

esto se hace cuando es resultado es indeterminado 0/0

para resolver un limite indeterminado hay dos casos:

A) Cuando no aparece raíces :Esta indeterminación se resuelve factorizando el numerador y denominador y simplificando.

B) Cuando aparece la raíces: En este caso debemos multiplicar por el conjugado y simplificarlo.

 

CONTINUIDAD DE UNA FUNCION

Intuitivamente decimos que una función es continua cuando podemos dibujarla con un sólo trazo del lápiz, es decir, sin levantar este del papel.

Discontinuidad

Las gráficas de la figura son discontinua en el punto x=a, y lo son por distintas razones. Las gráficas de 1 presentan asíntotas verticales (ramas infinitas) en x=a. Las de 2 presentan un salto finito en x=a. Las gráficas de 3 no tienen definido f(a), o, teniéndolo definido (caso de la derecha), no coincide con el valor en el entorno del mismo. En todos los casos resulta imposible dibujar las gráficas con un sólo trazo del lápiz, con lo que no son funciones continuas.

Tipos de discontinuidad:

• Discontinuidad evitable

  Se produce cuando existe el límite en el punto, y es finito, pero la función no está definida en él o, estándolo, tiene un valor distinto. Precisamente por eso se llama evitable: bastaría añadir o cambiar solo un punto para que la función fuese continua. Así pues

  1. limx→af(x)=k2. ∄ f(a) ó f(a)≠k
  

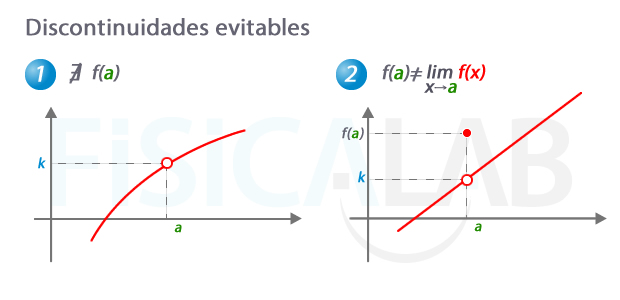
  Discontinuidad evitable

  Dos casos posibles de discontinuidad evitable. A la izquierda, en 1, existe el límite (k) pero no la función en a, lo cual se indica por el punto blanco en el trazado de la misma. A la derecha, en 2, la función está definida en a, pero no coincide con el valor del límite, k.

  Es habitual encontrar el primer caso en funciones racionales con raíces comunes en numerador y denominador (indeterminaciones del tipo 0/0), por ejemplo f(x)=x2−3xx−3 mientras que para el segundo es necesario acudir a las funciones a trozos, por ejemplo, f(x)={x0sisix≠3x=3 en x=3.

• Discontinuidad inevitable

  También conocida como discontinuidad esencial, se da cuando no existe el límite por no coincidir los límites laterales, o existiendo no es un valor finito. Podemos distinguir dos casos:

  • De salto finito

    Los límites laterales existen y son finitos, pero distintos. Es indiferente si la función está definida en el punto o no.

    limx→a−f(x)=klimx→a+f(x)=l  con k≠l y k,l∈R
    

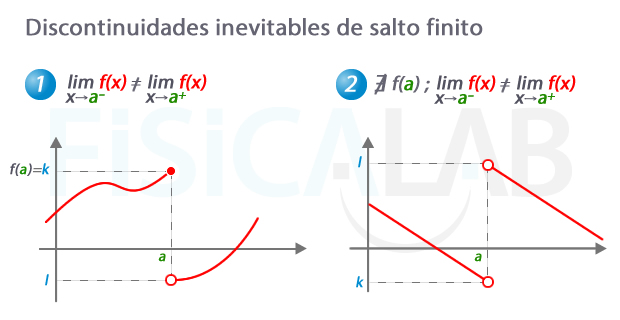
    Discontinuidad de salto finito

    Las gráficas de la figura son discontinuas en el punto x=a. Ambas presentan una discontinuidad de salto finito en él. En la gráfica de la función izquierda, la función está definida en el punto a pero no así en la de la derecha. La característica de este tipo de discontinuidad es que los límites laterales son finitos y distintos.

    Este tipo de discontinuidad es propia de funciones a trozos, y se da en los puntos de cambio de rama, por ejemplo, f(x)={xx2+1sisix≤0x>0 en x=0.

  • De salto infinito

    En este caso, al menos uno de los límites laterales es infinito. Este tipo de discontinuidades dan lugar a asíntotas verticales, por lo que también se llaman asintóticas.

    limx→a−f(x)=±∞ y/o limx→a+f(x)=±∞
    

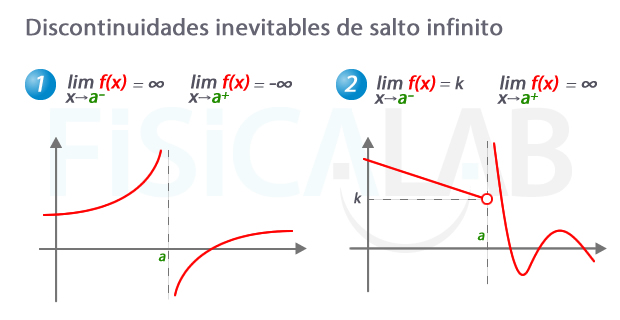
    Discontinuidad de salto infinito

    Las gráficas de la figura son discontinuas en el punto x=a. Presentan una discontinuidad asintótica o de salto infinito. En la gráfica de la función izquierda, los límites laterales son distintos, y por tanto, estrictamente hablando, ∄limx→af(x) (aunque, como sabes, se suele decir que limx→af(x)=∞). En la función de la derecha sólo es infinito uno de los límites laterales, el derecho. La característica de este tipo de discontinuidades es que al menos uno de los límites laterales es infinito.

Este tipo de discontinuidad es propia de funciones con asíntotas. Es el caso, por ejemplo, de funciones racionales con denominadores que se anulan que dan lugar a indeterminaciones del tipo k/0, como pueda ser f(x)=1/x en x=0.

limite de funciones trascendente:

limite de funciones trigonométricas: Para calcular estos limite tenemos que tener en cuenta limites notables y identidades trigonometrías.

 

LIMITES  NOTABLES TRIGONOMETRICO :

IDENTIDADES TRIGONOMETRICAS:

EJEMPLO:

Limite de funciones exponenciales :

Para ver el límite de funciones exponenciales, veamos primero este tipo de funciones.

Una función exponencial es del tipo: f(x) = k^x, siendo k un número positivo diferente de 1.

La variable de la función está en el exponente.

Si k es mayor que 1 (k > 1), la función exponencial es continua y estrictamente creciente en el dominio de los números reales. Si, por el contrario, k es menor que 1 (k < 1), la función es estrictamente decreciente.

 Podemos decir que los límites notables de estas funciones exponenciales son:

• Para k > 1:
  
• Para 0 < k < 1:
  

  
  

  
  

  

  
  

EJEMPLO:

MAPA CONCEPTUAL DE LIMITES

CONCLUSION :

El tema de limite nos ayuda a determinar los comportamientos de dichas funciones.

Podemos decir que para que un limite exista debe de tener sus limites laterales, a saber que: limite f(x) cuando x tiende a a por izquierda es = L, y el limite f(x) cuando x tiende a a por derecha = L 

HIPERVINCULO:

https://www.esap.edu.co/portal/wp-content/uploads/2017/10/5-Matematicas-i.pdf